中学数学とスポーツ
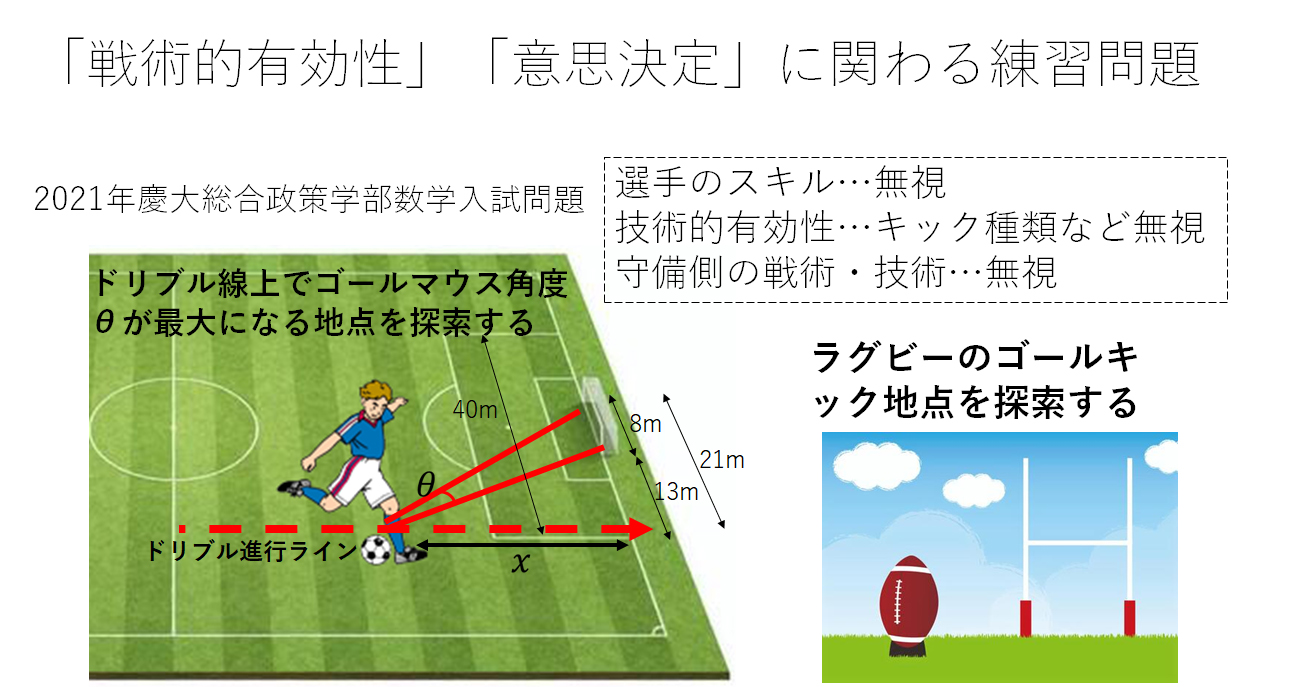
こうした数学問題が2024年にNHK番組「3か月でマスターする数学」で取り上げられた。
◆NHK「3か月でマスターする数学」第1回円周角(2024.6.26)
■2021年慶応大学総合政策学部入試(数学)
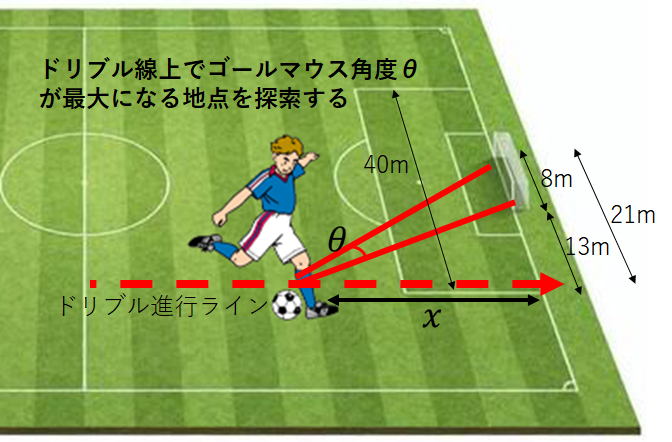 2021年の慶応大学入試問題に興味ある数学問題が出題されました。大学入試なので、高校数学「三角関数」を利用した解法でしたが、実はこの幾何学解法は中学数学を使っても可能です。
2021年の慶応大学入試問題に興味ある数学問題が出題されました。大学入試なので、高校数学「三角関数」を利用した解法でしたが、実はこの幾何学解法は中学数学を使っても可能です。
問題の意味は、ゴールラインに向かってドリブルで突進する中、ゴールマウス角度が最大となる地点がシューターにとっては最適になるので、その地点を求めるという問題です。数学問題ということで、実際には重要である選手のスキル、技術的有効性(どういったシュートキックを選択すればいいのか:グラウンダー、ループ、ボールへの回転の掛け方など)、当然ながら守備側、特にGK位置などといった要素はすべて無視し、シュートを蹴る選手から見たゴールマウス角度だけが最大となる位置を考えるという単純化。こうした単純化して物事をとらえることは、プレーの本質的理解を深めることにつながりますので、ジュニア期のプレーヤーにとって学校の勉強と一体化して取り組める意味で、非常に優れた教材でしょう。
水球でも全く同じ問題が作れます。

●中学数学での解法
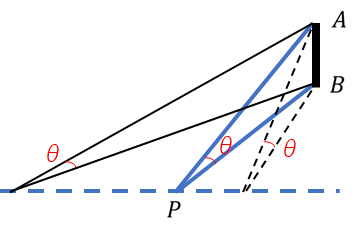 ドリブルコースの直線上に位置する点Pとゴールマウス幅(線分AB)とでできる三角形を考えて、∠APBの角度θを考えることになります。実際に点Pを直線上に動かしてみると、最適と思われる地点よりも線分ABから遠ざかっても近づいても角度θは小さくなります。これは経験上でも理解できます。角度の問題を中学数学で考える基本は円周角問題でしょう。この問題を円周角問題にするというのは、
ドリブルコースの直線上に位置する点Pとゴールマウス幅(線分AB)とでできる三角形を考えて、∠APBの角度θを考えることになります。実際に点Pを直線上に動かしてみると、最適と思われる地点よりも線分ABから遠ざかっても近づいても角度θは小さくなります。これは経験上でも理解できます。角度の問題を中学数学で考える基本は円周角問題でしょう。この問題を円周角問題にするというのは、
ゴールマウスの両端点ABを通り、ドリブルコース直線上に接する円を描くと、この円の接点位置で、線分ABとのなす角度θ(シュート選手から見たゴールマウス角度)が最大となる
という問題に置き換えるのです。
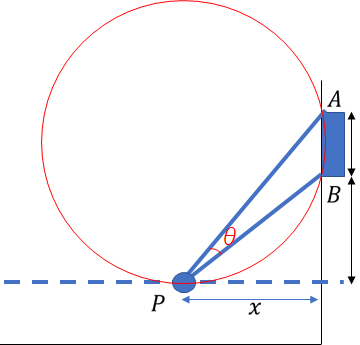
中学数学の図形問題の定番は「補助線」。この問題も補助線を引くことで理解が進む典型問題になります。
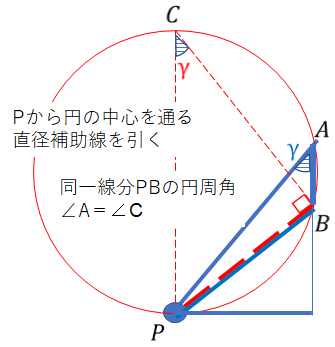
円周角の性質は中学数学でも学び、同一円内にある線分によって作られる円周角は同じです。この性質を使い、点Pから直径をなす補助線を引いて、線分BPと円でできる円周角を考えると、∠A=∠Cとなります。
この直径を底辺とする△CPBを考えると、
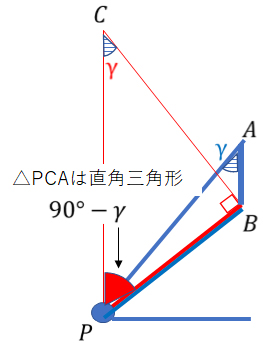
直角三角形の性質から、∠CPB=90°−円周角(γ)なので、
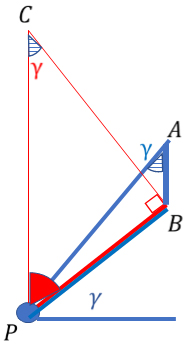
線分BPとドリブルコース直線とのなす角度も円周角(γ)ということになります。このことを整理すると、
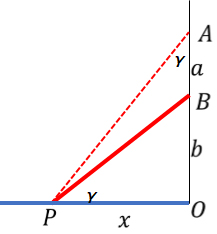
△AOPと△POBは「3つの角が等しい」という相似形になることが理解できます。相似形というわけで、各辺の長さは比例関係になりますので、

ということに落ち着きます。
水球シュート問題で考えると、計算結果は次の通り。

水球選手が「シュートできる!」と思う位置とかなり一致していることがわかりますよね。
こんなことと中学や高校の数学とが関係しているのです。
 2021年の慶応大学入試問題に興味ある数学問題が出題されました。大学入試なので、高校数学「三角関数」を利用した解法でしたが、実はこの幾何学解法は中学数学を使っても可能です。
2021年の慶応大学入試問題に興味ある数学問題が出題されました。大学入試なので、高校数学「三角関数」を利用した解法でしたが、実はこの幾何学解法は中学数学を使っても可能です。

 ドリブルコースの直線上に位置する点Pとゴールマウス幅(線分AB)とでできる三角形を考えて、∠APBの角度θを考えることになります。実際に点Pを直線上に動かしてみると、最適と思われる地点よりも線分ABから遠ざかっても近づいても角度θは小さくなります。これは経験上でも理解できます。角度の問題を中学数学で考える基本は円周角問題でしょう。この問題を円周角問題にするというのは、
ドリブルコースの直線上に位置する点Pとゴールマウス幅(線分AB)とでできる三角形を考えて、∠APBの角度θを考えることになります。実際に点Pを直線上に動かしてみると、最適と思われる地点よりも線分ABから遠ざかっても近づいても角度θは小さくなります。これは経験上でも理解できます。角度の問題を中学数学で考える基本は円周角問題でしょう。この問題を円周角問題にするというのは、





